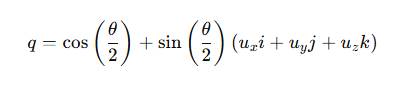Вращение объектов вокруг вектора- оси с помощью кватернионов

Загрузить проект С++ здесь ПРИМЕР КОДА 1 - в этом примере кватернион поворачивается на 90 градусов вокруг вектора оси Z затем преобразуется в матрицу поворота

Загрузить проект С++ здесь ПРИМЕР КОДА 2 - в этом примере кватернион поворачивается на 90 градусов вокруг произвольной вектора оси

Загрузить проект С++ здесь ПРИМЕР КОДА 3 - в этом примере кватернион поворачивается на 90 градусов вокруг вектора оси Y

Реализация в коде С++.

В примере ниже кватернион поворачивается на 90 градусов вокруг вектора оси Z затем преобразуется в матрицу поворота

#include <math.h>

#define PI 3.1415926535897932384626433L

struct Quaternion
{
    double w, x, y, z;

    Quaternion operator*(const Quaternion& q) const
	{
		Quaternion q_out = {       
            w * q.w - x * q.x - y * q.y - z * q.z,
            w * q.x + x * q.w + y * q.z - z * q.y,
            w * q.y - x * q.z + y * q.w + z * q.x,
            w * q.z + x * q.y - y * q.x + z * q.w
        };

		return q_out;
    }

    Quaternion conjugate() const
	{
		Quaternion q_out = {w, -x, -y, -z};
        
		return q_out;
    }
};

// Функция для создания матрицы вращения 4x4 из кватерниона
void createRotationMatrix4x4(const Quaternion& q, double matrix[4][4]) {
    double xx = q.x * q.x, yy = q.y * q.y, zz = q.z * q.z;
    double xy = q.x * q.y, xz = q.x * q.z, yz = q.y * q.z;
    double wx = q.w * q.x, wy = q.w * q.y, wz = q.w * q.z;

    matrix[0][0] = 1.0 - 2.0 * (yy + zz);
    matrix[0][1] = 2.0 * (xy - wz);
    matrix[0][2] = 2.0 * (xz + wy);
    matrix[0][3] = 0.0;

    matrix[1][0] = 2.0 * (xy + wz);
    matrix[1][1] = 1.0 - 2.0 * (xx + zz);
    matrix[1][2] = 2.0 * (yz - wx);
    matrix[1][3] = 0.0;

    matrix[2][0] = 2.0 * (xz - wy);
    matrix[2][1] = 2.0 * (yz + wx);
    matrix[2][2] = 1.0 - 2.0 * (xx + yy);
    matrix[2][3] = 0.0;

    matrix[3][0] = 0.0;
    matrix[3][1] = 0.0;
    matrix[3][2] = 0.0;
    matrix[3][3] = 1.0;
}

int main()
 {

    // Угол и ось вращения
    double theta = PI / 2; // 90 градусов
    Quaternion q = {cos(theta / 2), 0, 0, sin(theta / 2)};
    Quaternion p = {0, 1, 0, 0}; // Вектор (1, 0, 0)
    Quaternion q_inv = q.conjugate();

    // Вращение: p' = q * p * q^-1
    Quaternion p_rotated = q * p * q_inv;

    // Создание матрицы вращения 4x4
    double rotationMatrix[4][4];
    createRotationMatrix4x4(q, rotationMatrix);

    return 0;
}

Кватернион — это математическая структура, состоит из четырех компонентов.

struct quaternion
{
    float w, x, y, z;
};

Как видим подобно вектору кватернион состоит из компонент x,y,z и есть четвертая компонента w.

Основные операции с кватернионами:

• Сложение и вычитание- выполняются поэлементно
• Умножение- выполняется по правилам умножения мнимых единиц и распределительного закона
• Норма кватерниона (длинна по формуле Пифагора)
• Сопряжение
• Обратный кватернион- если норма не равна нулю

Применение кватернионов.

• Кватернионы применяются для представления вращений в трёхмерном пространстве без проблем, присущих матрицам поворота (например, эффекта "гимбаллок" — потери одной степени свободы).
• Единичный кватернион используется для вращений
• Для интерполяции поворотов (например, SLERP — Spherical Linear Interpolation)
• Для моделирования динамики твёрдого тела в физике

Для вращения объекта с помощью кватерниона, сначала по определенной формуле надо создать кватерниона вращения, далее из кватерниона вращения создать матрицу вращения, а потом можно вершины модели умножать на эту матрицу вращения.

Для вращения объекта в трёхмерном пространстве при помощи кватернионов используется формула:

	p1 = qpq-1

p¹ - кватернион, представляющий повернутую точку

q — единичный кватернион, задающий вращение

p — вектор, представляющий точку, которую нужно повернуть, записывается как чисто мнимый кватернион: p=0+xi+yj+zk

q⁻¹ - обратный кватернион для q

Кватернион вращения создается по следующий формуле, угол вращения Phi и ось вращения u_x, u_y, u_z: